Imagine you’re building a super tall tower out of blocks. As you stack the blocks higher and higher, you might notice that it starts to lean or sway a bit, especially if you push it lightly from the side. This leaning or swaying can cause the tower to become unstable and even collapse if you’re not careful. In the world of engineering and physics, this phenomenon is related to something called the “P-Delta Effect.”
What is the P-Delta Effect?
The P-Delta Effect is a concept used in structural engineering to describe how tall structures, like skyscrapers, can become less stable when they experience both vertical and horizontal forces at the same time. The term “P” stands for the vertical load or axial load (the weight of the structure and everything it supports), and “Delta” (Δ) represents the horizontal displacement (the movement or sway of the structure).
Breaking It Down
- Vertical Loads (P): Think of this as the weight of the building itself and everything inside it, like furniture, people, and equipment. This weight pushes straight down.
- Horizontal Displacement (Δ): This is how much the building sways or leans to the side. This can be caused by wind, earthquakes, or even slight imperfections in the construction.
- Combined Effect (P-Delta): When the building sways to the side (Δ) while still carrying all that weight (P), it creates extra stress on the structure. This additional stress can make the building more likely to bend or even collapse if not properly accounted for in the design.
A Simple Example
Let’s say you’re holding a long ruler vertically and pressing down on the top with your hand (this is like the vertical load, P). Now, if you push the middle of the ruler sideways with your other hand (horizontal displacement, Δ), you’ll notice that it bends more and becomes harder to keep straight. This bending is similar to what happens in a tall building experiencing the P-Delta Effect.
Why is P-Delta Important?
Understanding the P-Delta Effect is crucial for engineers who design tall buildings. If they didn’t consider this effect, a strong wind or minor earthquake could cause serious damage or even lead to a catastrophic failure of the structure. By calculating and planning for the P-Delta Effect, engineers can make buildings safer and more stable.
Let’s discuss P-Delta with a bit mathematically,
Imagine this is a simply supported vertical column. Both end “pin supported”. Now if an axial force P is applied at the column end. (Fig. a), there will be some stress, i.e., axial stress.
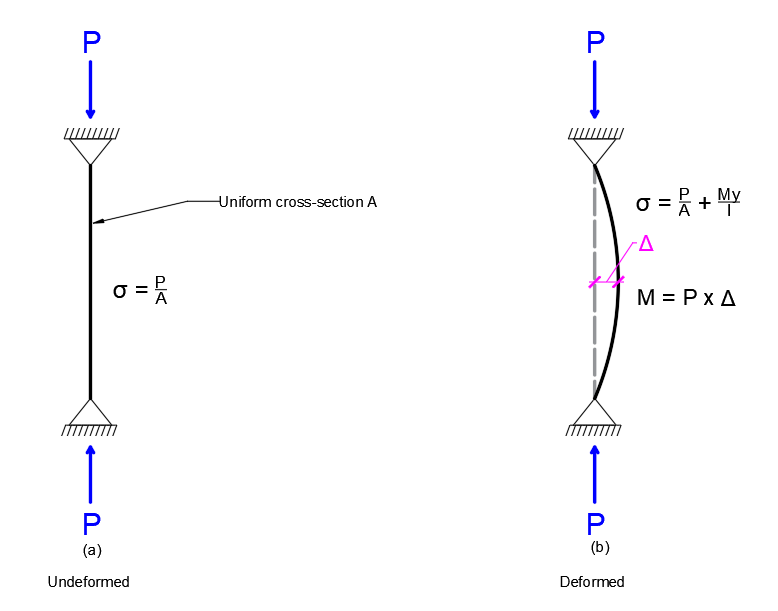
And what is the magnitude of this stress? For the axial load P and the column uniform cross-section A, the axial stress is simply P/A. So, based on this stress we will design this column and guess what? This is not a safe design. Why not?
Well, now the P-Delta effect has come into play.
Whenever this column is subjected to axial load P this will Buckle like this (Fig. b) and there will be a lateral displacement.
And initially the load was passed through this line (Fig. b dotted line), but now it is not. Consider, the displacement from this Center Line to this new position is Δ. In this particular cross section there are now two loads – first one is the axial load P, and the second one is a moment M = P x Δ.
For these two loads, two stresses will be generated; axial stress P/A and stress due to moment My/I, where I is the moment of inertia.
So, due to this displacement Δ, the structure will fail if we do not consider this extra stress My/I caused by the P-Delta effect.
Now let’s consider another case. Let’s say we have a cantilever column like (Fig. c) this.
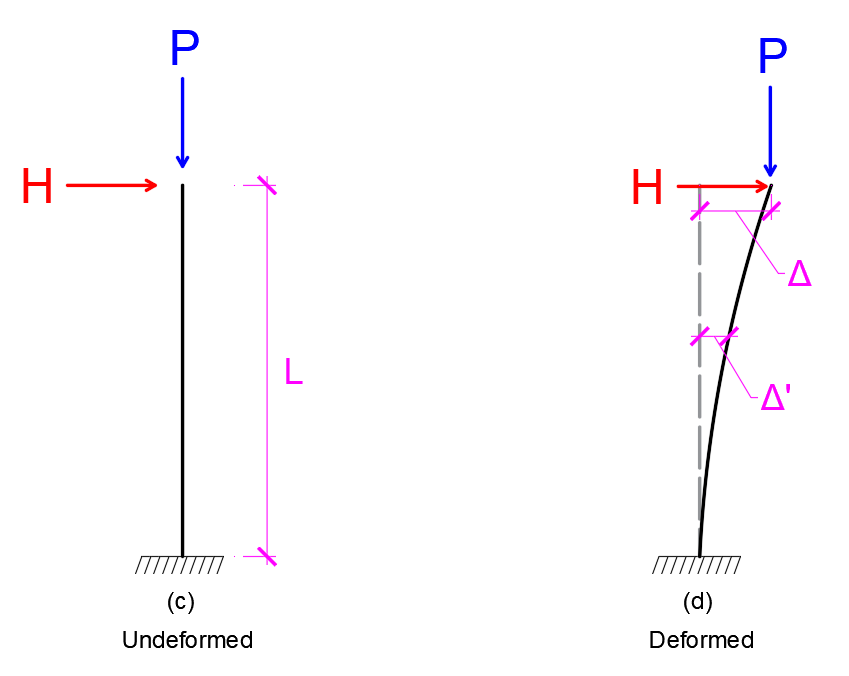
This column is subjected to an axial load P and a lateral load H. So, what will be the effect? Simply it will bend like this (Fig. d). Now at the very top there is let’s say total Δ displacement and somewhere in the middle, the displacement is Δ’ and at the bottom (fixed support) the displacement Δ is zero. Due to the displacement, the applied load is now acting at the displaced position.
Now, we draw the stress diagram due to this lateral load H and axial load P. For axial load this is simple. The diagram remains constant (P/A) throughout the column length.
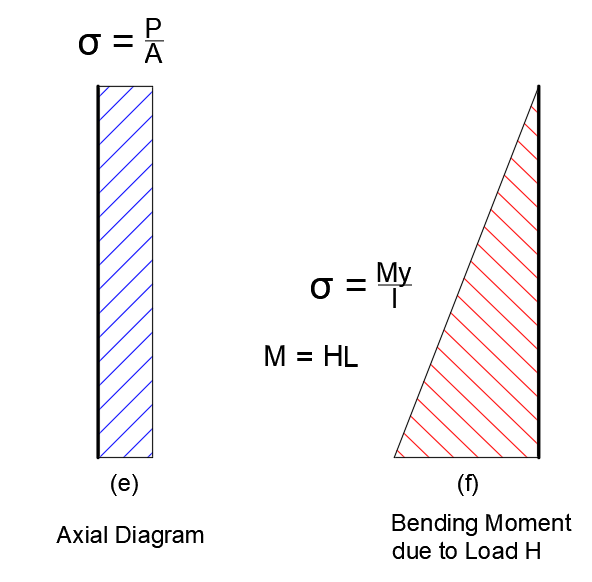
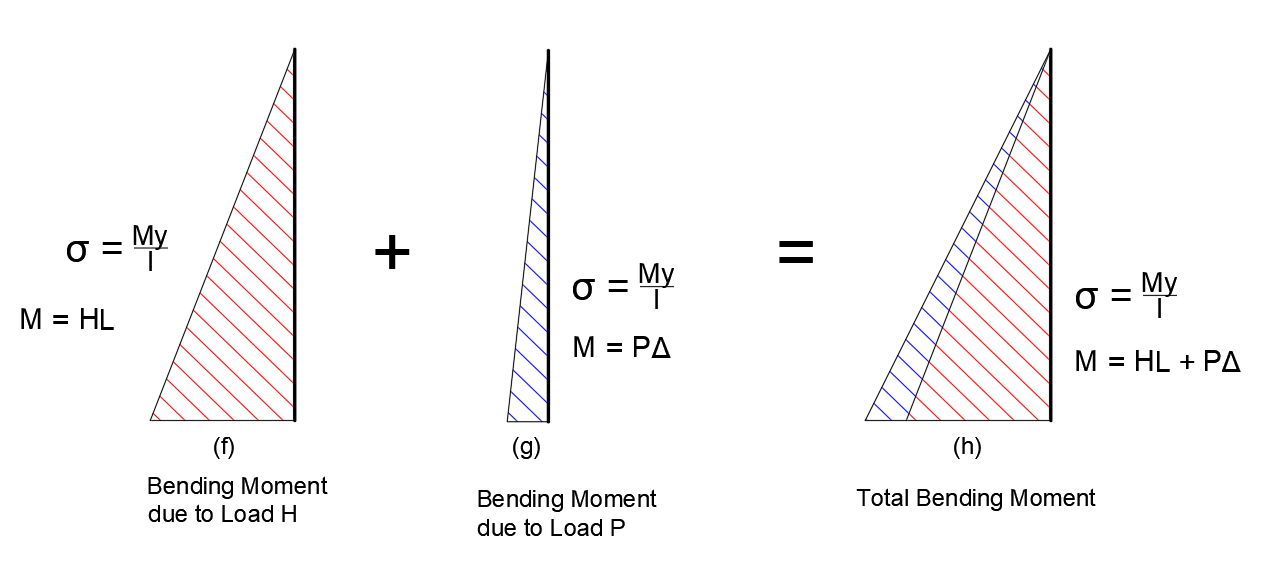
For the lateral load H, considering the length of the column is L, the bending moment diagram will be like this (Fig. f). At the top the moment is zero and at the bottom moment M = H x L, and varies linearly. So, at the bottom of this column the maximum stress is simply P/A due to the axial force and My/I due to bending moment.
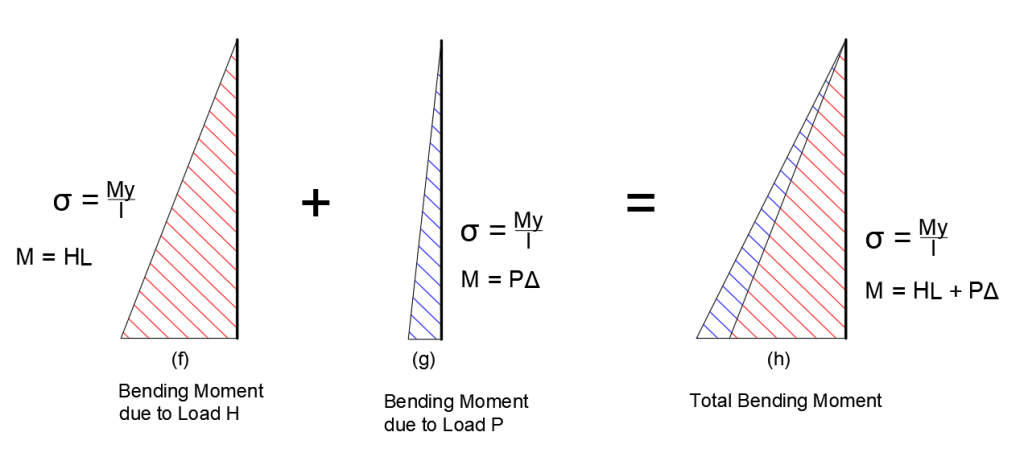
Based on this, if we design this column, the column will not be safe. Why? There needs to be considered another additional stress caused by the lateral displacement at the top due to the P-Delta effect and this act in the same direction along with the lateral load H.
Now, let’s say the direction of the axial force is upward. In this case, what will happen? The bending moment diagram will remain the same due to load H. But once it has displaced the P will have some counter moment due to this upward Direction. In that case we will have less bending moment at the base that is M = (HL – PΔ).
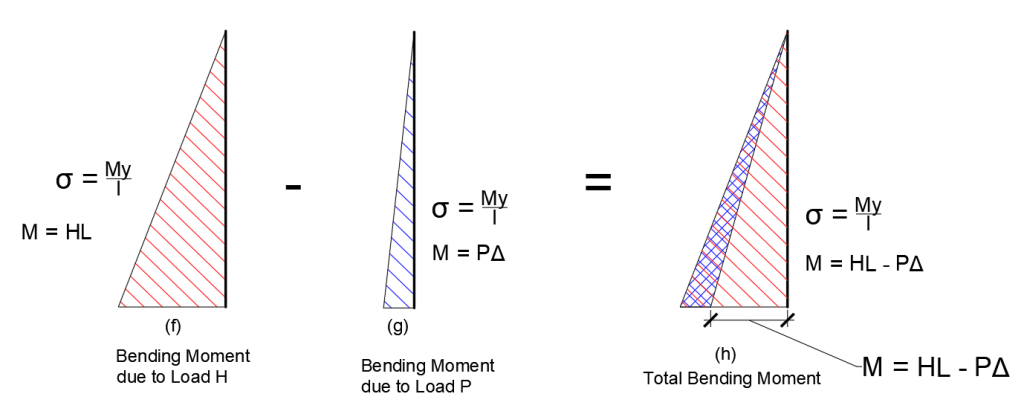
I think now it is clear why we should consider this P-Delta effect. Sometimes, it will help us to save material and sometimes it will help us to make the design safe.
How Do Engineers Handle P-Delta Effect?
Engineers use advanced mathematics and computer analysis to predict how much a building will sway and how that sway will affect its stability. They design the structure to be strong enough to handle these extra stresses. This might involve using stronger materials, adding extra support beams, or designing the building’s shape to be more aerodynamic to reduce sway.
Real-World Applications
- Skyscrapers: In places with strong winds or earthquakes engineers must design skyscrapers to withstand these forces. The P-Delta Effect is a big part of their calculations.
- Bridges: Long bridges, especially those over water, face similar challenges with wind and traffic loads. Engineers account for the P-Delta Effect to ensure these bridges remain safe and stable.
- Towers and Masts: Structures like radio towers and wind turbine masts also need to be designed with the P-Delta Effect in mind to prevent them from toppling over.
Conclusion
The P-Delta Effect might sound complicated, but it’s really about understanding how forces and movements work together to affect tall structures. By studying and planning for this effect, engineers can create buildings and bridges that are not only impressive but also safe and durable. So next time you see a skyscraper or a long bridge, you’ll know a bit more about the invisible forces that keep it standing tall!